1. 单源最短路径

1.1 Dijkstra算法

  给定一个有向图G = (V,E)，每条边(i,j)上都标有非负实数C[i][j]作为它的权；在图中指定一个顶点v作为源点，求从v到其他每个顶点的最短路径长度。

  为求最短路径，Dijkstra提出按路径长度的递增次序，逐步产生最短路径的“贪心”算法。权定义如下：

算法要点如下：

• 将V分成两个集合S(开始只有源点1)和V-S。其中，S是最短路径已经确定的顶点集合；V-S是最短路径尚未确定的顶点集合。每一步从V-S中选一个顶点w加入S，使得S中从源点到其余顶点的路长最短，直到V-S为空为止。
• 设数组D记录从源点到其余各顶点的最短路径长度，则w可归纳选取如下：
  • 归纳基点：令S包含源点1；D[i]=C[1][i]
  • 归纳假设：设S包含k个顶点，其中v1=1，并且D[v1],D[v2]...D[vk]最小
  • 归纳选取：在V-S中选取一个顶点w，使经过{v1,v2...vk}中某个顶点而到达w的路径长度最短
       D[w]=min(D[v]+C[v][w]，其中v是S中，w是V-S中)

代码如下：

void Dijkstra(C)    {        S = {1};        for(i=2;i<=n;i++) {            D[i] = C[1][i];        }        for(i=1;i<=n-1;i++) {            从V-S中选出一个w使得D[w]最小；            把w加入S；            for(V-S中每个顶点v)                 D[v] = min(D[v],D[w]+C[w][v]);        }    }

1.2 Bellman-Ford算法

采用邻接表

  先介绍一下松弛技术。对于每个结点v来说，我们维持一个属性v.d，用来记录从源结点s到结点v的最短路径权重的上界。我们称其为最短路径估计。

先初始化：

INITIALIZE-SINGLE-SOURCE(s) {        for each vertex v in V            v.d = infinity;        s.d = 0;    }

进行松弛：

//w存储着边长，s为源点    RELAX(u,v,w) {        if v.d > u.d + w(u,v)            v.d = u.d + w(u,v);    }    //经过松弛后，改善了v点的最短路径估计

Bellman-Ford算法：

BELLMAN_FORD(w,s) {        INITIALIZE-SINGLE-SOURCE(s);        for i = 1 to |V| - 1            for each edge(u,v)                RELAX(u,v,w);        for each edge(u,v)            if(v.d > v.d+w(u,v))                cout << "you fu huan lu a!";    }

2. 每一对顶点的最短路径

2.1 FLoyd算法

  为了求出每一对顶点之间的最短路径，可以令图中的每个顶点作为源点，n次重复利用Dijkstra算法即可，复杂性为O(n³)。但对每对顶点间的最短路径的更直接的算法是利用Floyd算法。虽然其时间复杂性也是一样，但是步骤很简单。而且实际效率也更高

  Floyed对邻接矩阵进行处理，其定义和Dijstra一样。定义A[i][j]是i到j的最短路径长度，P[i][j]来记录经过的顶点。

• 原理：对矩阵A共进行n遍处理。令i为矩阵A的行下标，表示一条路径的起点；j为列下标，表示终点，当第k遍处理时，A[i][j]的值由如下公式确定：

     A_k[i][j] = min{ A_k-1[i][j], A_k-1[i][k] + A_k-1[k][j] }

• 代码

void Floyd(A,C,n)     {        for(i=1;i<=n;i++) {            for(j=1;j<=n;j++) {                A[i][j] = C[i][j];                P[i][j] = 0;            }        }                for(k=1;k<=n;k++) {            for(i=1;i<=n;i++) {                for(j=1;j<=n;j++) {                    if(A[i][k] + A[k][j] < A[i][j]) {                        A[i][j] = A[i][k]+A[k][j];                        P[i][j] = k;                    }                }            }        }    }            void Path(i,j)    {        k = P[i][j];        if(k!=0) {            Path(i,k);            cout << k << endl;            Path(k,j);        }    }

2.2 Warshall算法

这个算法主要是用于求两个点是否是可达的，即判断i到j是否有一条有向路径

  这里邻接矩阵的定义为：

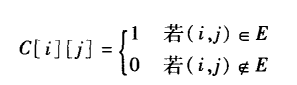
自己到自己是可达的

  矩阵A，有一条路径从i到j时，A[i][j]=1；否则，就有A[i][j]=0。通常把矩阵A称为邻接矩阵C的传递闭包。用C0表示邻接矩阵，以后每次加入一个顶点来构造C1，C2...Cn。

有两个规则：

• 如果A[i][j]在Ck-1中为1，则在Ck中也为1
• 如果A[i][j]在Ck-1中为0，当且仅当A[i][k]和A[k][j]都为1时，A[i][j]在Ck中才变为1

只需对Floyd算法稍作修改：

初始化A[i][j]为邻接矩阵            for(k=1;k<=n;k++) {        for(i=1;i<=n;i++) {            for(j=1;j<=n;j++) {                A[i][j] = A[i][j] ∪ (A[i][k] ∩ A[k][j]) ;            }        }    }

Dijkstra算法是贪心策略，所以图中不能有负权值的边，FLoyd-WarShall算法为动态规划策略，故可以存在负权值的边，但是不能有负权值的环路，而Bellman-Ford允许有负权值的边，且当图中有负权值的环路时会检测出来。

3. 有向图的中心点

设d[i][j]表示从i到j的最短距离。对于任意一个顶点k，称：

    E(k) = max{ d[i][j] }，其中i in V

为顶点k的偏心度。而称偏心度最小的顶点为中心点。

直接利用Floyd算法即可算出